Design with XOR/XNOR#
Recall the XOR and XNOR logic gates and expressions.
\(\Large A \oplus B = \bar{A}B + A\bar{B}\)

\(\Large \overline{A \oplus B} = AB + \bar{A}\bar{B}\)

These conditions occur so commonly that they have their own dedicated ICs, which can greatly simplify logic circuits.
Example
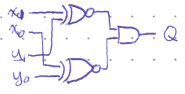
Design a logic circuit that will check the equality of two 2-bit binary numbers. Given inputs \(X_1X_0\) and \(Y_1Y_0\), the circuit should output high if they are equal and low otherwise.
First, we construct the truth table.
\(X_1\) |
\(X_0\) |
\(Y_1\) |
\(Y_0\) |
Q |
|---|---|---|---|---|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Now we create a Sums of Products expression and simplify.
If we were to draw this circuit as written it would be quite complicated with 4 NOT gates, 5 AND gates, and 2 OR gates. But recognizing the XNOR operation in each of the bracketed terms, the circuit simplifies to just three gates.