Flip Flop Applications

Flip flops have many uses in digital electronics. It would be hard to find an everyday digitial device that didn’t have a flip flop somewhere. In the next few sections we will list some of the common use-cases of flip flops (excluding at the beach).

Detecting an Input Sequence

Consider two signals \(A\) and \(B\) where know each signal will go from low to high at some point, but we would like to know the order in which this happens. We can use a D flip flop to tell use the order by putting one signal into the data input and the other into the clock.

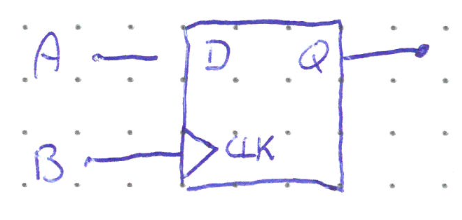
Look at the difference in output \(Q\) depending on the order in which the inputs go high.

This type of sequence detector is often used when detecting clockwise or counterclockwise rotation of an adjustment knob (e.g. a volume knob on a speaker), and can be the basis for electronic combination locks.

Detecting a Transition

Suppose there is some signal \(A\) where the value itself isn’t really important, but knowing when the value changes is important. For example, when tracking rotary motion as the motor moves from one side to another. It doesn’t really matter what orientation the motor is in, but knowing how fast it is switching (i.e. how far apart the transitions are) can be useful. We want a signal that is high for a brief period of time only when the signal \(A\) switches states.

A D flip flop with a relatively fast clock, combined with an XOR gate, is the simplest way to accomplish this task. As long as \(A\) does not change back and forth faster than the clock, the output \(Q\) will follow \(A\) through its changes with a slight delay since \(Q\) will only change on an active transition. By XORing \(Q\) with the original signal, you get a result that is high for a very short period of time (less than the clock period) after each transition from \(A\).

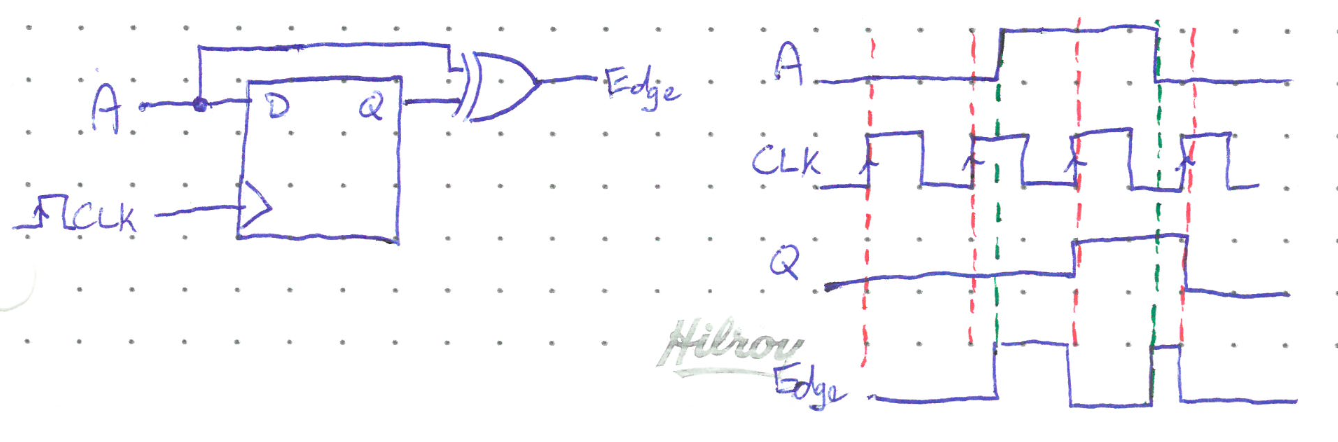
Data Storage and Transfer

Arguably the most far-reaching property of flip flops are their ability to remember and store data. Memory in a computer is made of groups of flip flops called registers. Using a universal clock, it is easy to transfer the data from one register to another register in a different location (say from memory to the CPU).

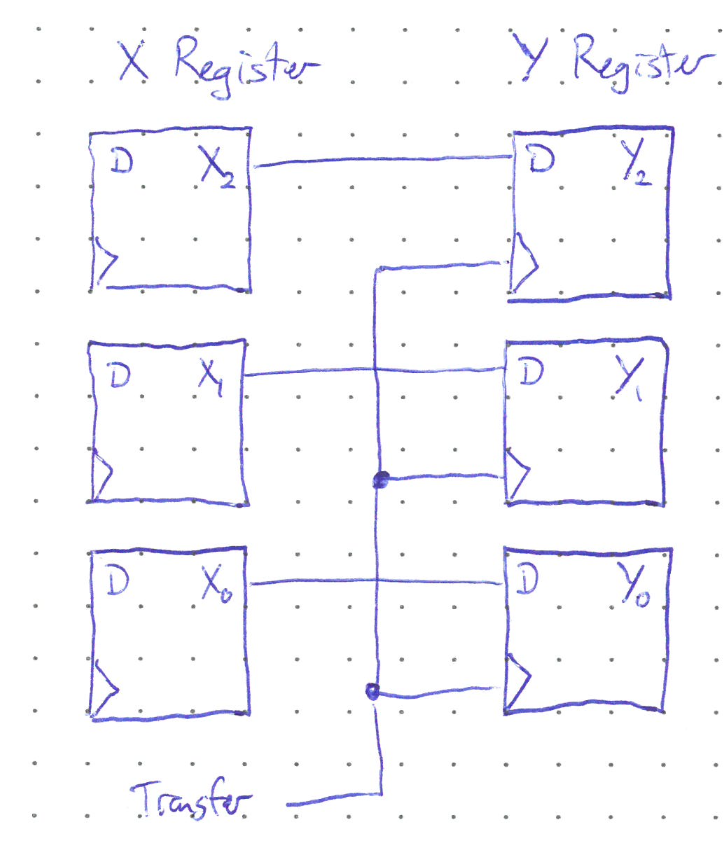
The transfer can either be done in parallel, where each flip flop in the first register transfers their data simultaneously to a flip flop in the other register when the transfer signal is sent.

Or, the transfer can be done serially, where every flip flop tranfers its data to the one next to it, with only the last flip flop in one register tranferring to the first input of the other. For the example shown below, it would thus take three shift pulses to fully transfer the three bits from the X Register to the Y Register.

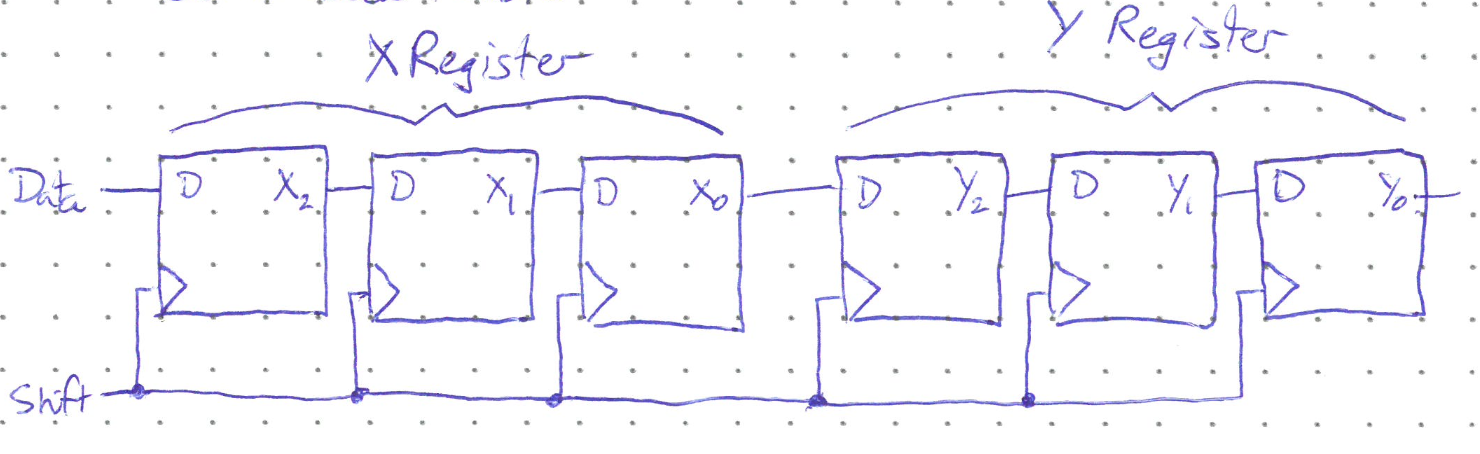
Because the flip flops have to read the value from the previous flip flop before it changes, shift registers are made with short hold times compared to the propagation delays.

Obviously, parallel data transfer is much faster than serial transfer, but serial transfer is simpler and less likely to break if there is a long distance between registers. Many register ICs will have options for a combination of methods such as Parallel In/Serial Out.

Frequency Division

Consider the following arangement of JK flip flops where the output from one flip flop is used as the clock signal for the next, and all \(J\) and \(K\) inputs are held high (i.e. in toggle mode).

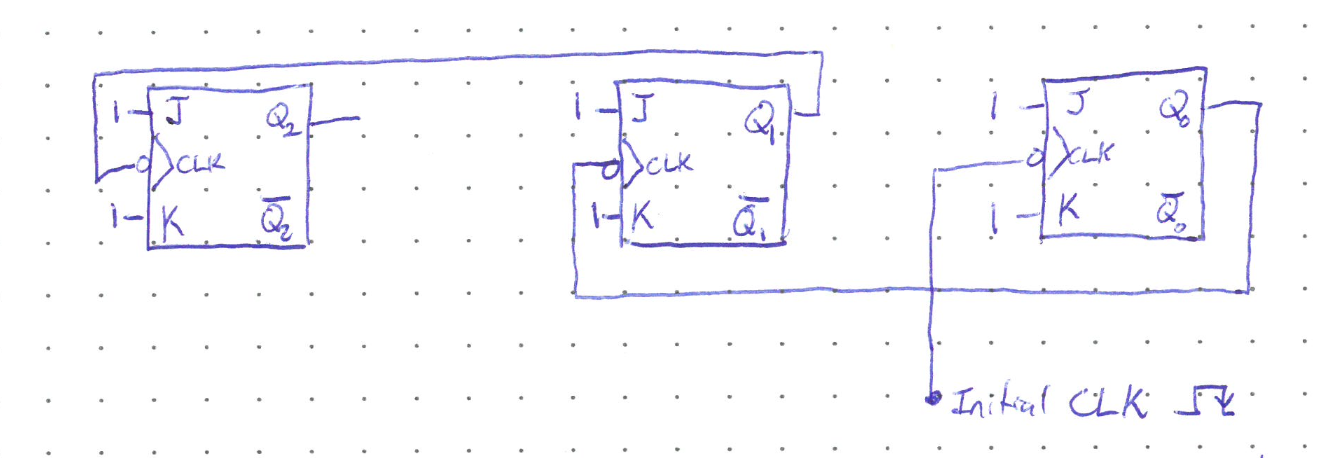
The timing diagram is shown below if all flip flops were initially in the high state. By looking from the clock to \(Q_0\) to \(Q_1\) to \(Q_2\) output signals, we can see that the frequency is halved with each successive flip flop. The final \(Q_2\) output wave has a period that is eith times that of the original clock.

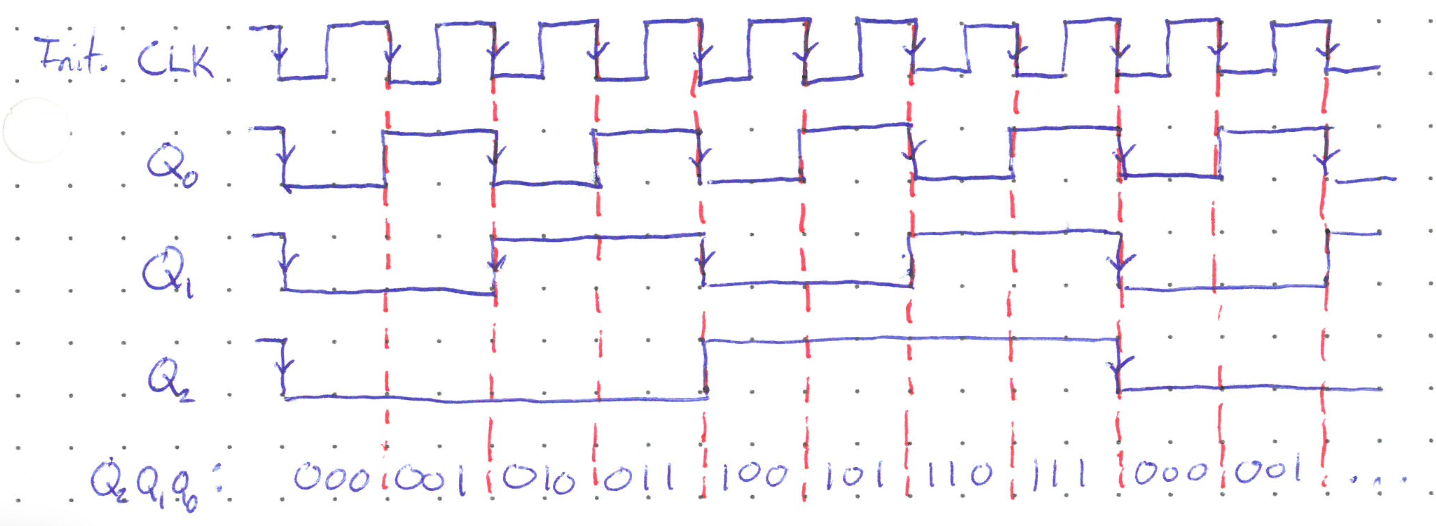
What is very interesting though, is to consider \(Q_2Q_1Q_0\) together as a binary number. We can see that, with each active transition of the original clock, that number ticks up by one. The number counts up all the way from 0 to 7, then starts over again and repeats ad nauseum.

Concept Check:

How high can \(N\) flip flops count?

Solution

Each flip flop adds one bit to the binary number. Recall that the maximum value of an N-bit binary numbery is \(2^N -1\).