NOR, NAND, XOR, and XNOR#
Some combinations of operations are done so often that they are given their own logic gate and have specialized integrated circuits (ICs) to perform them. Remember these are not part of Boolean algebra, but are created from the three fundamental operations.
NOR and NAND are the negations of OR and AND respectively (e.g. NAND is an AND gate followed immediately by a NOT gate).
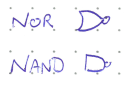
XOR is an exclusive OR operation. It will be True only when exactly one input is True, but not both. In an algebraic expression, we represent an XOR operation with a \(\oplus\) symbol. Its negation is called XNOR.
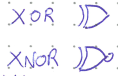
Here is a table summarizing the composite gates functionality.
\(\Large A\) |
\(\Large B\) |
\(\Large\overline{A + B}\) |
\(\Large\overline{AB}\) |
\(\Large A \oplus B\) |
\(\Large\overline{A \oplus B}\) |
|---|---|---|---|---|---|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
NOR and NAND can have multiple inputs just like OR and AND, but you should only ever use two inputs at a time with XOR gates to avoid confusion.
Example:
Suppose you had a circuit with three inputs \(A\), \(B\), and \(C\) and wanted the output to be high only if exactly one input is high. Use a truth table to show that \(A \oplus B \oplus C\) (the naive reading of an XOR gate with three inputs) would not lead to the desired result.
\(A\) |
\(B\) |
\(C\) |
\(A \oplus B\) |
\((A \oplus B) \oplus C\) |
Only one of A, B, C high |
|---|---|---|---|---|---|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
Notice that \(A \oplus B \oplus C\) yields high when all of A, B, and C are high, which is not what we wanted out of the circuit.
